A Nash equilibrium is a state in game theory where no player can increase their payoff by changing their strategy unless all other players change their strategies. Simply put, it's a stable game outcome in which each player acts in their own best interests, assuming that others will also act in their own interests.

John Nash proved the existence of such an equilibrium in mixed strategies in any finite game:



Payoff matrix at the Nash equilibrium:



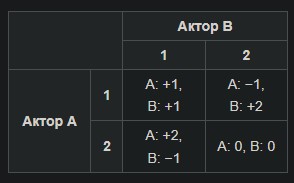
Examples

1) Factorio



This is a logic game, with very little randomness, and everything that typically happens or doesn't happen to you in Factorio is your doing or not doing. You can, for example, make it 2.1 using modules, but it won't affect the overall outcome. 

2) Heroes 3



You might get something good from the box, something not quite good, or nothing at all. Either the morale of units during a battle can ruin a guard break, for example, and you'll lose your entire army. Or, conversely, morale can save the game at the right time, or a box, or even a magic cast, or a drop from the Dragon Utopia, etc. 

Heroes is more about randomness and luck, although some logic in the actions is also present. 

3) Prison Poker 



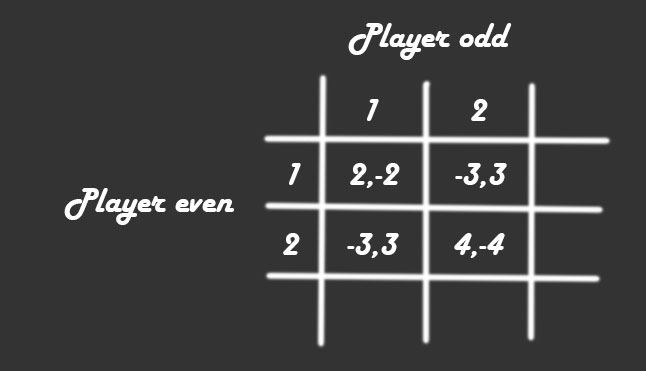
Player even - even player, player odd - odd player .

Game rules:

Two people play. On the count of three, they must show one or two fingers. Depending on the total number of fingers, the player on the even and odd sides wins. If there are two or four fingers in total, the player on the even side wins. If there are three, the player on the odd side wins. 

In the screenshot above, you can see the winning matrix for even and odd players. This is usually played for money: 
 

• Player even - $2, $4.
• Player odd - $3.

It would seem that this is a simple game like tossing a coin, the one who comes up wins. But no way:

Prison poker is not a Nash equilibrium

In it, one side will always lose, and the other will always win, regardless of the game strategies.

Mathematical calculations in respect to John Nash:
 

• 1/2 [1] + 1/2 [2] - we are tossing a coin.

The odd player's winnings (player odd) for the strategies of showing one and two fingers:
 

• Player odd (odd) [1] = 0.5 (-2) + 0.5 x 3 = -1 + 1.5 = 0.5
• Player odd (odd) [2] = 0.5 x 3 + 0.5 (-4) = 1.5 - 2 = -0.5 

The game is considered unfair if, in equilibrium, on average, one of the players wins against the other.
Finding the true equilibrium in prison poker, where the odd player (player odd) always wins: 
 

• Player odd (odd) [1] = -2p + 3(1-p)
• Player odd (odd) [2] = 3p - 4(1-p)
• p = 7/12 or 7/12 [1] + 5/12 [2] 

To consistently win at prison poker, the odd player (Player odd) needs to show one finger 7 out of 12 times and two fingers 5 out of 12. 
q = 7/12 is the probability for odd, slightly more often showing one finger than two.

The winnings for even and odd players with this strategy: 
 

• Player even = -1/12
• Player odd = +1/12 

An odd player in prison poker will, on average, win 1/12 of an even player's money. That is, If you play 120 games on the odd side, you can win $10; if you play 1200 games, you can take $100 from the even side, and so on. 

Now the main question: why am I telling you all this? 

Conclusion:

When choosing which game to play, or if you're offered to play something, you can apply a simple filter: 
 

• you're offered a logic game like Factorio or chess, for example.
• You're offered a game of dice rolling and randomness like in Heroes 3, a game of luck.
• You're offered a game of prison poker on the even side, which will always lose to the odd side.

In the case of logic and randomness games, you can choose a suitable strategy for winning, and in the case of prison poker, you can refuse to play or agree, but only on the odd side. As a rule, in this case, the opponent will not play against you if they are on the even side, because if they didn't know the mechanics, they wouldn't offer you to play this poker game.