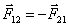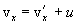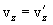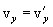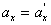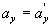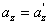Принцип относительности. Третий закон Ньютона

Третий закон Ньютона

Третий закон Ньютона формулируется следующим образом:

Две материальные точки действуют друг на друга с силами, которые численно равны между собой и направлены во взаимно противоположные стороны вдоль прямой, соединяющей эти точки:

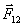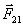Следует отметить, что силы  и  приложены к разным телам и поэтому не уравновешивают друг друга.

Принцип относительности Галилея

Равномерное и прямолинейное движение (относительно какой-либо инерциальной системы отсчета) замкнутой системы не влияет на закономерности протекания в ней механических процессов.

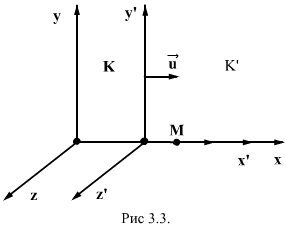
Рассмотрим две системы отсчета: неподвижную (К) и движущуюся относительно первой вдоль оси Х с постоянной Х с постоянной скоростью 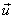 (K’). Координаты тела М в системе К x:y:z , а в системе К’ - x’:y’:z’. Эти координаты связаны между собой соотношениями, которые называются преобразованием Галилея

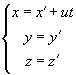
Дифференцируя эти уравнения по времени и учитывая, что 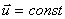, найдем соотношения между скоростями и ускорениями:

Таким образом, если в системе К тело имеет ускорение а, то такое же ускорение оно имеет и в системе К’.

Согласно второму закону Ньютона:

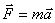
т.е. второй закон Ньютона одинаков в обоих случаях.

При 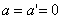 движение по инерции, т.о., справедлив и первый закон Ньютона, т.е. рассматриваемая нами подвижная система является инерциальной. Следовательно, уравнения Ньютона для материальной точки, а также для произвольной системы материальных точек одинаковы во всех инерциальных системах отсчета - инвариантны по отношению к преобразованиям Галилея.

Следовательно, в механике все инерциальные системы отсчета совершенно равноправны. Поэтому никакими механическими опытами внутри системы нельзя обнаружить движется ли система равномерно и прямолинейно или покоится.