Импульс системы и уравнение динамики поступательного движения

Второй закон Ньютона, через импульс системы

Используя выражение для импульса

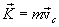
и второй закон Ньютона можем записать

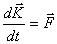 (3.11)

где 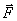 - главный вектор всех внешних сил, действующих на систему.

Последнее уравнение является обобщением уравнения импульса на произвольную механическую систему, т.к. ее всегда можно представить, в виде системы материальных точек, взаимодействующих друг с другом и с внешними телами. Внешними телами называются тела, не входящие в состав рассматриваемой системы, а силы, действующие на систему со стороны этих тел - внешними силами.

Соответственно силы взаимодействия между материальными точками, принадлежащими рассматриваемой системе называются внутренними силами, и их равнодействующая равна нулю. Уравнение (3.11) показывает, что скорость изменения импульса механической системы равна главному вектору всех внешних сил, действующих на эту систему.

Уравнение динамики поступательного движения

Используя уравнения:

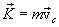 и

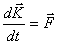
можем записать

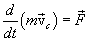
или

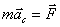 (3.12)

Таким образом, центр инерции механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору внешних сил, приложенных к системе.

В общем случае движение твердого тела можно рассматривать как сумму двух движений: поступательного со скоростью 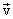, равной скорости  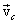центра инерции тела, и вращения вокруг центра инерции. Поэтому последнее уравнение часто называют основным уравнением динамики поступательного движения твердого тела.

Источник: physics-lectures.ru.