Криволинейное равномерное движение тела

При прямолинейном движении векторы скорости и ускорения совпадают с направлением траектории. Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости в любой точке траектории направлен по касательной к ней. Допустим, что в т.М траектории скорость была 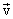, а в т.М1 стала .

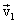При этом считаем, что промежуток времени при переходе точки на пути 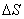 из М в М1 настолько мал, что изменением ускорения по величине и направлению можно пренебречь. Для того, чтобы найти вектор изменения скорости 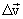, необходимо определить векторную разность:

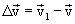
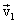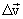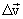Для этого перенесем  параллельно самому себе, совмещая его начало с точкой М. Разность двух векторов равна вектору, соединяющему их концы  равна стороне АС  МАС, построенного на векторах скоростей, как на сторонах. Разложим вектор  на две составляющих АВ и АД, и обе соответственно через  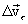и 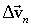. Таким образом вектор изменения скорости  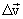равен векторной сумме двух векторов:

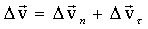
По определению:

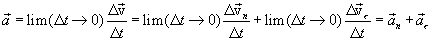 (1.15)

Тангенциальное ускорение 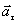 характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории. Следовательно: 

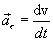 (1.16)

Нормальное ускорение 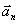 характеризует быстроту изменения скорости по направлению. Вычислим вектор:

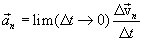
Для этого проведем перпендикуляр через точки М и М1 к касательным к траектории (рис. 1.4) Точку пересечения обозначим через О. При достаточно малом 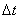 участок криволинейной траектории можно считать частью окружности радиуса R. Треугольники МОМ1 и МВС подобны, потому, что являются равнобедренными треугольниками с одинаковыми углами при вершинах. Поэтому:

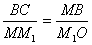
или

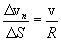
Но 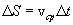, тогда:

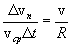
Переходя к пределу при 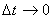 и учитывая, что при этом 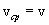, находим:

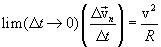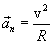,  (1.17)

Так как при 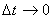 угол 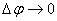, направление этого ускорения совпадает с направлением нормали к скорости 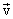, т.е. вектор ускорения  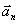перпендикулярен 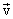. Поэтому это ускорение часто называют центростремительным. Полное ускорение определяется векторной суммой тангенциального нормального ускорений (1.15). Так как векторы этих ускорений взаимноперпендикулярны, то модуль полного ускорения равен:
 

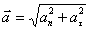 (1.18)

Направление полного ускорения определяется углом между векторам 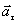 и :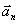

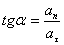
Источник: physics-lectures.ru.