Центростремительное ускорение. Линейная и угловая скорость

Центростремительное ускорение

В случае неравномерного движения 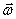 не остается постоянной. Величина, характеризующая скорость изменения угловой скорости называется угловым ускорением и равна:

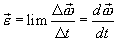 (2.5)

В случае вращения тела вокруг неподвижной оси изменение вектора 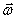 обусловлено только изменением его численного значения. При этом вектор  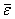углового ускорения направлен вдоль оси вращения в ту же сторону, что и  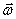при ускоренном вращении  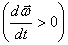и при замедленном  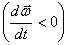в обратном направлении (рис. 2.3 а,б).
 

Линейная и угловая скорость

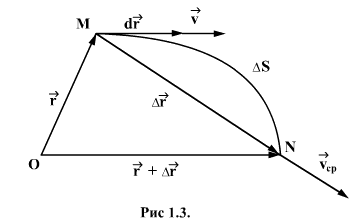
Отдельные точки вращающегося тела имеют различные линейные скорости . Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление.

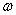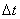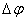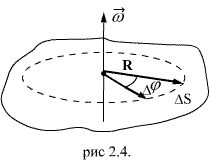
Величина скорости  определяется скоростью вращения тела  и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени  тело повернулось на угол 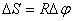 (рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный

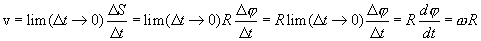
Линейная скорость точки по определению:

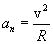 (2.6)

Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:

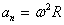
подставляя значение скорости из (2.6), находим:

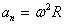 (2.7)

Тангенциальное ускорение

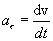
Воспользовавшись тем же отношением (2.6) получаем

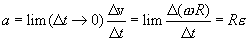 (2.8)

Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения.

Источник: physics-lectures.ru.